Von Archimedes zu William Froude

Auch bei den heutigen anspruchsvollen Entwurfsaufgaben spielen die wissenschaftlichen Grundlagen, die von Archimedes bis Froude geschaffen wurden, eine wesentliche Rolle. Professor Horst Nowacki beschreibt anhand der Arbeiten der wichtigsten Forscher die Geschichte eines Zusammenwirkens von Theorie und Praxis im Schiffsentwurf
1. Einleitung

Der Anlass des 150. Jubiläums der Gründung der maritimen Zeitschrift HANSA regt zu historischen Betrachtungen an[ds_preview], auch über die Geschichte des Zusammenfindens von Schiffbaupraxis und Schiffbauwissenschaft. Archimedes und William Froude sind zwei herausragende Wissenschaftler, die bahnbrechende Beiträge der Wissenschaft zur Schiffbaupraxis geleistet haben. Am Beispiel ihrer Arbeiten zur Sicherheit und Wirtschaftlichkeit von Schiffen soll die Geschichte eines Zusammenwirkens von Theorie und Praxis beleuchtet werden, das heute zu einer unentbehrlichen Tradition geworden ist. Die Wege und Umwege dieser Entwicklungen führen über einen Zeitraum von mehr als zweitausend Jahren. Die Darstellung muss daher skizzenhaft bleiben, soll aber wesentliche Erkenntnisse herausarbeiten, auf denen wir heute noch aufbauen.

Archimedes verdanken wir die physika­lischen Grundlagen zur Bestimmung von Auftrieb und Verdrängung sowie der hydro­statischen Gleichgewichtsschwimmlage des Schiffes und die Bewertung seiner Stabilität mit dem Begriff Hebelarm. Diese Begriffe sind grundlegend für die Schiffssicherheit, und dies auch in vielen anderen Anwendungsszenarien.

Auf William Froude geht die Begründung des Schiffbauversuchswesens mit einer praxisfähigen Methodik zur Prognose des Verhaltens der Großausführung auf der Basis von Modellversuchen zurück. Widerstand und Antriebsleistung für eine Schiffsform können so in der Entwurfsphase vorhergesagt und durch Formgebungsmaßnahmen verbessert werden. Gleiches gilt auch für andere Merkmale der hydrodynamischen Leistungsfähigkeit des Schiffes wie beim Manövrieren oder im Seegang. Mit diesen Prognosen werden wesentliche Aspekte der Wirtschaftlichkeit des Schiffes, aber auch seiner Sicherheit, messbar und bewertbar gemacht.

Beide Beiträge sind im Sinne moderner Naturwissenschaft wissenschaftlich fundiert, indem sie, ausgehend von wenigen Axiomen, durch Beobachtung und Messung relevante Eigenschaften des Schiffes in der Entwurfsphase quantifizierbar machen. Das ermöglicht rationale Entwurfsentscheidungen.

Mehr als zwei Jahrtausende liegen zwischen Archimedes und Froude. Auch vor William Froude gab es bereits Schiffsmodellversuche, aber noch keine Methodik zur Extrapolation auf die Großausführung. Erst um etwa 1870 wurden die Grundlagen dafür vollständig geschaffen. Man fragt sich also, warum es so lange brauchte, um praxisreife Anwendungen hervorzubringen. Diesen Weg will der vorliegende Artikel in knapper Form darstellen.

Die Entwicklung ging inzwischen aber noch wesentlich weiter und hat heute zu einer modernen, integrierten Sicht auf den gesamten Entwurfsprozess geführt. Wenn man heute im integrierten, ganzheitlichen Schiffsentwurf auf alle Leistungsmerkmale und Sicherheitskriterien gleichzeitig eingeht, etwa nach der Methodik des »Risk Based Ship Design«, dann basiert dieser Bewertungsprozess nach wie vor auf den Grundlagen, die von Archimedes und William Froude geschaffen wurden.

Für interessierte Leser, denen die knappe Darstellung hier nicht ausreicht, sei auf zwei weitere Publikationen des Verfassers verwiesen ((H. Nowacki: »Archimedes and Ship Design«, Beitrag zur International Conference on »Archimedes in the 21st Century«, New York University, 31. Mai/1.Juni 2013, organisiert von Prof. Chris Rorres. Nachdruck in: Preprint 445 des Max-Planck-Instituts für Wissenschafts­geschichte, Berlin, 2003.), (H. Nowacki: »Zur Vorgeschichte des Schiffbauversuchswesens«, Beitrag zum Sprechtag des FA Geschichte des Schiffbaus der STG, Bremerhaven, November 2013. Abgedruckt im STG-Jahrbuch 2013.)), welche auch zahlreiche weiterführende Literaturangaben enthalten.

2. Archimedes

Archimedes lebte von ca. 287 bis 212 v. Chr. in Syrakus. Er wird von vielen als der hervorragendste Mathematiker, Mechaniker und Ingenieur der Antike angesehen. Seine erhalten gebliebenen Schriften bestechen durch ihren axiomatischen Aufbau, ihre brillante Klarheit und ihre zwingende Logik. Sie können daher noch heute als moderne Grundlagen von Mathematik und Naturwissenschaft gelten. Dies gilt insbesondere auch für seine Schriften zur Hydro­statik schwimmender Systeme.

Für maritime Anwendungen in der Hy­drostatik ist das zentrale überlieferte Werk des Archimedes die Schrift »Über schwimmende Körper« ( , »On Floating Bodies« / OFB (A. Czwalina-Allenstein: »Abhandlungen von Archimedes«, übersetzt und kommentiert von Czwalina-Allenstein, 1922, Ostwalds Klassiker der exakten Wissenschaften, Band 201, Verlag Harri Deutsch, 1996.), (»Archimedes Werke«, übersetzt und kommentiert von A. Czwalina, mit einem Anhang einschließlich von »Die Methode«, übersetzt von J. L. Heiberg, nachgedruckt von Wissenschaftliche Buchgesellschaft, Darmstadt, 1967.)), die bestimmte frühere Schriften zum Hebelgesetz und zur Geometrie einfacher Körper voraussetzt, die auch erhalten sind. Die Reihenfolge seiner erhaltenen Schriften ist gut rekonstruiert worden (siehe auch (H. Nowacki: »Archimedes and Ship Design«, Beitrag zur International Conference on »Archimedes in the 21st Century«, New York University, 31. Mai/1.Juni 2013, organisiert von Prof. Chris Rorres. Nachdruck in: Preprint 445 des Max-Planck-Instituts für Wissenschafts­geschichte, Berlin, 2003.)).

In OFB befasst sich Archimedes mit den Gleichgewichtsaxiomen für ruhende, schwimmende Systeme. Aus dem Kräftegleichgewicht leitet er das fundamendale Archimedische Prinzip (Auftrieb V= Verdrängungsgewicht , = spez. Gew. der Flüssigkeit, V= eintauchendes Volumen) her, das für teilweise oder voll eingetauchte Körper beliebiger Form gilt. Das Axiom des Momentengleichgewichts führt zu Krite­rien für die hydrostatische Stabilität des ruhenden Körpers, die er für Spezialfälle homogener Festkörper einfacher Form begründet. Anwendungen auf Schiffe, ja, das Wort Schiff, kommen in seinen Schriften nirgends vor, worin ein wenig die platonisch-griechische Distanz zu konkreten, praktischen Beispielen durchscheint. Aber da das Schiff ein Spezialfall eines schwimmenden Systems ist, gelten die Prinzipien der Hydrostatik auch für Schiffe.

2.1 Das Archimedische Prinzip

Das Grundgesetz der Hydrostatik für einen ruhenden Körper, der an der Oberfläche oder im Innern einer homogenen Flüssigkeit schwimmt, wird von Archimedes in seiner Schrift OFB, Buch I, strikt mithilfe eines Gedankenexperiments hergeleitet. Es gilt für einen Körper beliebiger äußerer Form. In OFB, Buch I, § 1, setzt Archimedes voraus, dass die Flüssigkeit aus Teilchen besteht, sodass jedes Teilchen vom Gewicht aller Teilchen, die vertikal über ihm liegen, nach unten gedrückt wird. Heute würde man dann von einer hydrosta­tischen Druckverteilung sprechen. Sodann behauptet er:

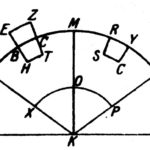
»Ein Körper taucht in einer spezifisch schwereren Flüssigkeit so weit ein, dass das Volumen der von ihm verdrängten Flüssigkeit so viel wiegt wie der gesamte Körper.« Er beweist dies in OFB, Buch I, § 5, kurz und elegant (Abb. 1):

• Die Oberfläche einer ruhenden Flüssigkeit ist eine Kugel, deren Mittelpunkt der Erdmittelpunkt ist.

• Betrachten wir zwei gleiche Nachbarsektoren, berandet durch die Oberflächen LM und MN. Der erste Sektor enthält den schwimmenden Körper, dessen getauchter Teil BHCT ist. Der zweite Sektor hat stattdessen ein gleiches Flüssigkeitsvolumen RSCY.

• Die Flüssigkeit ruht. Daher erfahren die Flächen an den unteren Randabschnitten XO und OP gleiche Gewichtslasten. Deswegen sind die Gewichte der Volumina über diesen Flächen gleich. Aber das Gewicht des ersten Sektors ohne den Raum BHCT ist gleich dem Gewicht des zweiten Sektors ohne den Raum RSCY. Daher muss das Gewicht des Körpers EZTH gleich dem Gewicht des Flüssigkeitsvolumens RSCY sein. Die verdrängte Flüssigkeit wiegt also so viel wie der gesamte Körper.

Der Beweis ist rein deduktiv, ausgehend von wenigen axiomatischen Annahmen.

2.2 Stabilitätskriterien

Von Archimedes stammen auch die ersten wissenschaftlichen Kriterien für die hydrostatische Stabilität schwimmender Körper. In OFB, Buch II, untersucht er die Stabiltät des Momentengleichgewichts eines einfachen, homogenen Schwimmkörpers an den Beispielen der Kugel und des Rotationsparaboloids. Zur Herleitung benutzt er wieder ein Gedankenexperiment:

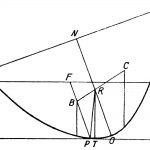
• Der Körper wird durch Krängung in eine geneigte Lage gebracht (Abb. 2).

• Anschließend bildet sich ein Kräftepaar aus der Auftriebskraft durch den Volumenschwerpunkt B des getauchten Körperteils nach oben und der Gewichtskraft durch den Gewichtsschwerpunkt R des Festkörpers nach unten. Die Lage dieser Schwerpunkte kennt Archimedes aus geometrischen Betrachtungen an der gegebenen Körperform, und zwar unter Berücksichtigung der Volumenverschiebung von den austauchenden zu den eintauchenden Keilstückvolumina durch die Krängung (Schwerpunktverschiebungssatz des Archimedes).

• Wenn nun die beiden parallelen, aber entgegengesetzt gerichteten Kräfte zwischen ihren Wirkungslinien ein aufrichtendes Moment bilden, d. h., wie man sagt, einen aufrichtenden Hebelarm haben, wird der Körper zur aufrechten Lage zurückgeführt, sprich: seine Schwimmlage ist stabil. Der Hebelarm bzw. das aufrichtende Moment ist also für Archimedes das Stabilitätskriterium im hydrostatischen Fall.

Obwohl die Stabilitätsuntersuchung des Archimedes auf einfache Formen von Festkörpern beschränkt ist, lässt sich doch sein Grundgedanke, den Hebelarm als Stabilitätskriterium im hydrostatischen Fall zu verwenden, ohne Weiteres auf Schiffe ausdehnen, wie später geschehen.

Mit seinen Ergebnissen von OFB legte Archimedes die Grundlagen für das Gleichgewicht und die Stabilität schwimmender Körper. Ansätze zur Bestimmung von Form- und Gewichtsschwerpunkten sowie Schwimmlagen und Hebelarmen waren ihm geläufig. Es fehlten aber damals noch numerische Verfahren und eine geschlossene Darstellung der Schiffsgeometrie, um diese Erkenntnisse quantitativ auf praktische Schiffsformen anzuwenden. Auch waren die belastenden Einflüsse durch Wind und Seegang noch nicht für den Entwurf quantifizierbar.

Das Wissen des Archimedes ging bald nach seinem Tod für die Wissenschaft und erst recht für die Praxis verloren, da seine Schriften nur an wenigen Stellen gesammelt worden waren und dort oft verbrannten oder abhanden kamen. Dass überhaupt einzelne seiner Schriften für die Nachwelt erhalten geblieben sind, grenzt an ein Wunder.

2.3 Die Überlieferung

Die Schriftrollen und Pergamente mit Abschriften von Manuskripten des Archimedes waren in der Spätantike noch zahlreicher vorhanden als im Mittelalter, wie man aus Zitaten weiß (Heron, Pappos). Heute liegen noch zwölf seiner Schriften vor, teils im griechischen Original (Codices A und C), teils in lateinischer Übersetzung (Codex B) (s. (H. Nowacki: »Archimedes and Ship Design«, Beitrag zur International Conference on »Archimedes in the 21st Century«, New York University, 31. Mai/1.Juni 2013, organisiert von Prof. Chris Rorres. Nachdruck in: Preprint 445 des Max-Planck-Instituts für Wissenschafts­geschichte, Berlin, 2003.)).

Nachdem in Alexandria viele Originale durch Brand und Plünderungen verloren gegangen waren, war das Byzantinische Reich der Raum, in dem man noch die meisten Kopien von Schriften des Archimedes vorfinden konnte. Dort wurde im 9. Jahrhundert eine Sammlung der noch auffindbaren Schriften durchgeführt. Zwei Abschriften dieser Manuskripte wurden im 11. Jahrhundert von byzantinischen Klerikern mit ins Exil nach Sizilien genommen. Dazu gehörte der griechische Codex A, der mehrfach kopiert wurde, ehe er verloren ging. Beide Manuskripte landeten nach dem Niedergang der Hohenstaufen, also nach 1266, in der Vatika­nischen Bibliothek. Dort standen sie dem Dominikaner Van Moerbeke zur Verfügung, der daraus schon 1269 in Viterbo eine lateinische Übersetzung herstellte, den Codex B, worin auch OFB enthalten war. Nach etwa 1500 wurden mit der Verbreitung der Druckerpresse zahlreiche Nachdrucke beider Codices zugänglich gemacht, nach 1600 auch Übersetzungen in moderne Sprachen. Der Zugriff auf OFB beruhte also viele Jahrhunderte nur auf der lateinischen Fassung, nachdem die griechischen Originalquellen verschollen waren.

Es existierte jedoch noch ein drittes griechisches Manuskript, das zunächst im 10. Jahrhundert wohl in Byzanz zu einem Palimpsest verarbeitet worden war, d. h. nach Abwaschen des Archimedes-Textes mit einem orthodox-griechischen Gebetbuch überschrieben worden war. Dieser Codex C wurde erst um 1900 im Metochion-Kloster in Konstantinopel wiederentdeckt und von Heiberg 1906 als Quelle mit unterliegendem, meist noch lesbarem Text als Archimedes-Quelle erkannt, transkribiert und übersetzt (J. L. Heiberg: »Archimedis Opera Omnia cum Commentariis Eutocii«, Griechisch u. Lateinisch, incl. »De Corporibus Fluitantibus« und »De Mechanicis Propositionibus ad Eratosthenem Methodus«, Leipzig, 1910, 1913, 1915.). Hierin ist auch OFB im griechischen Originaltext enthalten. Dieses Manuskript ging in den Wirren des griechisch-türkischen Krieges von 1920 bis 1922 erneut verloren und tauchte erst 1998 aus franzö­sischer Hand auf einer Auktion in New York, noch weiter stark beschädigt, wieder auf. Der anonyme Erwerber beauftragte das Walters Art Museum in Baltimore mit einer wissenschaftlichen, akribisch und mit modernsten Mitteln durchgeführten erneuten Rekonstruktion, die inzwischen abgeschlossen ist und in zwei Folianten vorliegt (W. Noel / R. Netz / N. Tchernetska / N. Wilson (Hg.): »The Archimedes Palimpsest«, 2 Bde., Walters Art Museum, Cambridge University Press, Cambridge, UK, 2011.). Die Grundaussagen des Archimedes zur Hy­drostatik schwimmender Körper bleiben davon unberührt.

2.4 Die Neuzeit

Vom 15. bis zum 17. Jahrhundert wurde der Zugang zu OFB über Codex B durch Nachdrucke sehr erleichtert. Gleichzeitig erschienen in den führenden Schiffbauländern, speziell in England (Bourne, Deane), Frankreich (Hoste) und Holland (Stevin, Hudde, Witsen, Van Yk), zahlreiche Fachschriften, die auf Archimedes’ Prinzip beruhten, ihn erwähnten und numerisch auf Schiffe anwandten (s.(H. Nowacki: »Archimedes and Ship Design«, Beitrag zur International Conference on »Archimedes in the 21st Century«, New York University, 31. Mai/1.Juni 2013, organisiert von Prof. Chris Rorres. Nachdruck in: Preprint 445 des Max-Planck-Instituts für Wissenschafts­geschichte, Berlin, 2003.)).

Besonders erwähnt sei hier der flämisch-holländische Physiker Simon Stevin (1548–1620), der die Hydrostatik auf der Grundlage von Archimedes wiederbelebte und um das Konzept des hydrostatischen Druckes bereicherte. Er wandte, über Archimedes hinausgehend, die Hydrostatik auch bereits auf Schiffe an (S. Stevin: »De Beghinselen des Waterwichts« (Elements of Hydrostatics), Niederländisch, Leyden, 1586, lateinische Übersetzung in: S. Stevin: »Hypomnemata Mathematica«, Leyden, 1608. Nachgedruckt in: E.J. Dijksterhuis (Hg.): »The Principal Works of Simon Stevin«, Bd. I, Mechanics, C. V. Swets & Zeitlinger, Amsterdam, 1955. Auch in diesem Bd.: S. Stevin: »De Beghinselen der Weegkonst« (Elements of the Art of Weighing), Niederländisch, Leyden, 1586, dritter Teil des Anhangs: »On the Floating Top-Heaviness«.).

Der holländische Physiker Christiaan Huygens (1629–1695) verfasste bereits im Jahr 1650, also im Alter von 21 Jahren, eine dreibändige, lateinische Schrift zur Stabi­lität schwimmender Körper, in der er die Ergebnisse des Archimedes nach einer eigenen Methode bestätigte, um weitere Beispiele geometrischer Körperformen erweiterte und auf 360 Grad Drehung ausdehnte. Seine Schrift blieb auf seinen Wunsch lange unveröffentlicht und erschien erst 1908 in seinen gesammelten Werken (Ch. Huygens: »De iis quae liquido supernatant libri 3«, 1650, publiziert in: Œuvres Complètes de Christiaan Huygens, Bd. XI, 1908, nachgedruckt von Swets & Zeitlinger N.V., Amsterdam, 1967.).

Nach 1700 gab es bereits stetige Schiffsformdarstellungen durch Linienrisszeichnungen, und die Anwendung der Infinitesimalrechnung breitete sich aus. Zwischen 1740 und 1750 waren es schließlich fast gleichzeitig und unabhängig voneinander Pierre Bouguer (1698–1758) und Leonhard Euler (1707–1783), die mit ihren fundamentalen Werken »Traité du Navire« (P. Bouguer: »Traité du Navire, de sa Construction et de ses Mouvemens [sic!]«, Jombert, Paris, 1746.) und »Scientia Navalis« (L. Euler: »Scientia Navalis seu Tractatus de Construendis ac Dirigendis Navibus«, St. Petersburg, 1749, aus Opera Omnia, Bd. 18/19, Zürich, 1967.) den Durchbruch zur modernen Hydrostatik für Schiffe schafften, indem sie für eine stetig definierte Schiffsgeometrie mithilfe der Integralrechnung ein vollständiges, numerisches Verfahren zur Bestimmung von Auftrieb und Stabilität von Schiffen in beliebiger Schwimmlage entwickelten.

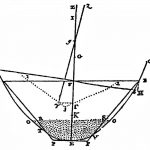
Bouguer verdanken wir den Begriff des Metazentrums als Kriterium für die Anfangsstabilität (Abb. 3). Euler verwendete als Stabilitätskriterium das aufrichtende Moment bzw. dessen Hebelarm wie Archimedes, auch für endliche Neigungen in Krängung und Trimm. Beide zeigten auch weitere Lösungen für viele andere Anwendungen der Schiffsstabilität und Bewegungsdynamik (H. Nowacki: »Archimedes and Ship Design«, Beitrag zur International Conference on »Archimedes in the 21st Century«, New York University, 31. Mai/1.Juni 2013, organisiert von Prof. Chris Rorres. Nachdruck in: Preprint 445 des Max-Planck-Instituts für Wissenschafts­geschichte, Berlin, 2003.). Mit den Arbeiten von Chapman (F. H. Chapman: »Traktat om Skepps Byggeriet« (»Treatise on Shipbuilding«), auf Schwedisch, 1775, frz. Übersetzung von Vial du Clairbois, Paris, 1781, deutsche Übersetzung von G. Timmermann, Hamburg, 1972.) und Atwood mit Vial du Clairbois (G. Atwood and H.-S. Vial du Clairbois: »A Disquisition on the Stability of Ships«, Phil. Trans. of the Royal Soc. of London, Bd. 88, 1798, S. vi-310.) ist belegt, dass hydrostatische Stabilitätsuntersuchungen schon vor 1800 im praktischen Schiffsentwurf einzelne Anwendung gefunden haben. Eine Wende zur routinemäßigen Nutzung kam erst mit dem Übergang zum größeren, risikoreicheren dampfangetriebenen Schiff aus Eisen und Stahl.

3. Das Versuchswesen

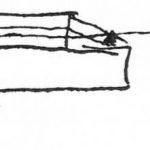
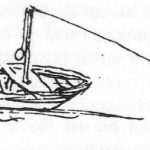
Die wissenschaftliche Entwicklung des Schiffsversuchswesens begann im Jahr 1669 mit Christiaan Huygens in Paris. Huygens lebte von 1663 bis 1681 in der französischen Metropole und war Gründungsmitglied der Académie des Sciences seit 1666. Er erhielt die Aufgabe, die Ausflussgesetze von Torricelli nachzuprüfen, die umstritten waren, und die Struktur des Widerstandsgesetzes für einen Körper in gleichförmiger Anströmung zu untersuchen. Dazu führte er 1669 mit verschiedenen Apparaturen mehrere Versuchsreihen durch, um den Widerstand einfacher Körper bei stationärer Geschwindigkeit zu messen. Dazu gehörten Schleppversuche mit einem Quader in einem Tank von ca. 3 m Länge, am Seil von einem fallenden Gewicht gezogen (Abb. 4a) sowie später im strömenden Fluss, der Seine, von einem verankerten Boot aus, wobei der angeströmte Körper am Seil durch Gewichte in einer Waagschale im Gleichgewicht gehalten wurde (Abb. 4b). Nach dem Umkehrprinzip lieferten beide Anordnungen unter den gleichen Umständen die gleichen Ergebnisse. Die Zeit wurde mit einem Halbsekundenpendel und der Weg durch Auszählung markierter Strecken in der stationären Versuchsphase gemessen (Ch. Huygens: »Expériences de 1669 sur la force de l’eau ou de l’air en mouvement et sur les résistances éprouvées par des corps traversant ces milieux«, persönliche Notizen von Huygens über seine 1669 angestellten Versuche, hg. und postum veröffentl. von Jean-Baptiste du Hamel, Geschichte der Académie Royale des Sciences, Paris, 1698. Wieder veröffentl. in: Œuvres Complètes, Bd. 19, Huygens an der Académie des Sciences, Dutch Soc. of Sciences, Martinus Nijhoff, Den Haag, 1937.). Nach mehreren Versuchsreihen mit verschiedenen Körpern bei unterschiedlichen Geschwindigkeiten kam Huygens zu der Folgerung, dass der Widerstand R des Körpers proportional zum Quadrat der Geschwindigkeit V und zu einer charakteristischen Fläche A (z. B. Querschnittsfläche) ist: R ~ V2 · A. Bei Versuchen in Luft mit querangestellten Platten kam Huygens zu dem gleichen Ergebnis.

Edmé Mariotte (1620–1684), Thermo­dynamiker und Strömungsphysiker, ebenfalls Gründungsmitglied der Académie des Sciences, hatte als Partner von Huygens an einigen von dessen Versuchsreihen teilgenommen und später eigene Versuche mit ähnlichen Apparaturen in Wasser und in Luft durchgeführt. Die Ergebnisse von Huygens wurden dadurch für Platten und andere Strömungskörper bestätigt (E. Mariotte: »Traité du mouvement des eaux et des autres corps fluides«, postum hg. und veröffentl. von Philippe de la Hire, Estrenne Michallet, Paris, 1686.).

Beider Physiker Ergebnisse wurden in Protokollen festgehalten, aber erst nach ihrem Tod gegen Ende des Jahrhunderts publiziert. Sie waren Newton also wahrscheinlich noch unbekannt, als er 1686 die erste Auflage seiner »Principia« (I. Newton: »Philosophiae Naturalis Principia Mathematica«, 1. Auflage, Cambridge, 1687, 2. Aufl., Cambridge, 1713, 3. Aufl., London, 1726. Deutsch übersetzt und hg. von Volkmar Schüller: »Die mathematischen Prinzipien der Physik«, Walter de Gruyter Publ., Berlin / New York, 1999.) schrieb. Darin kommt Newton auf anderem Wege zum gleichen Schluss für die Struktur des Widerstandsgesetzes mit dem eingliedrigen Ansatz R ~ · V2 · A. Dieser Ansatz ist nicht geignet für die Bildung mehrerer, kausal unterschiedlicher Widerstandsanteile und damit für die Ex­trapolation von Versuchsergebnissen.

Von Newton und den drei Auflagen von seiner »Principia« (I. Newton: »Philosophiae Naturalis Principia Mathematica«, 1. Auflage, Cambridge, 1687, 2. Aufl., Cambridge, 1713, 3. Aufl., London, 1726. Deutsch übersetzt und hg. von Volkmar Schüller: »Die mathematischen Prinzipien der Physik«, Walter de Gruyter Publ., Berlin / New York, 1999.) stammen wichtige Grundlagen der Widerstandsforschung, so z. B. wegweisende Ansätze über die Mate­rialeigenschaften von Fluiden (Trägheit, Schwere und Zähigkeit) und für die Anfänge der Ähnlichkeitsmechanik (für Trägheitskräfte). Für das Widerstandsgesetz leitete er für Körper in einem fiktiven, »dünnen« Medium (»rare fluid«) – d. h. einem Medium mit so wenigen, kleinen Masse­elementen, dass diese sich in ihrer Bahn nicht gegenseitig beeinflussen, sondern entweder elastisch vom Körper abprallen oder im unelastischen Fluid seitlich tangential zur Körperoberfläche abfließen – die sogenannte Stoßtheorie (»impact theory«) her. Nach dem Impulssatz ergeben sich durch Bilanz über die Vorderseite des Körpers Widerstandsbeiwerte. Auf die Rückseite gelangen nach dieser Theorie aber keine Teilchen, sodass diese nichts zum Widerstand beiträgt.

Diese irrige Hypothese wurde bald da­rauf von Daniel Bernoulli ((D. Bernoulli: »Hydrodynamica sive de viribus et motibus fluidorum commentarii« (Hydrodynamik oder Kommentare über die Kräfte und Bewegungen von Fluiden«), Straßburg, 1738.), 1738) und durch die ballistischen Versuche von Benjamin Robins ((B. Robins: »New Principles of Gunnery«, 1742, nachgedruckt in: Mathematical Tracts, London, 1761.), 1742) mit Artillerie­geschossen in Luft widerlegt. Aber es gab zunächst keinen praktischen Ersatz. Euler (L. Euler: »Scientia Navalis seu Tractatus de Construendis ac Dirigendis Navibus«, St. Petersburg, 1749, aus Opera Omnia, Bd. 18/19, Zürich, 1967.), Laplace u.a. entwickelten zwar potenzialtheoretisch ein realistischeres Strom­linienmodell, das aber in idealer Flüssigkeit den Widerstand null lieferte. Das Dilemma löste sich erst im Laufe eines weiteren Jahrhunderts im Zusammenwirken von Versuch und Theorie.

Obschon in den Folgejahren weitere Schiffsmodellversuche angestellt wurden, z. B. von Van Zwijndrecht, Borda, Théve­nard, Chapman, Bossut u. a., und sich die Versuchstechnik, meist mit fallenden Gewichten, weiter vervollkommnete, fehlte es weiterhin an einer praktikablen Methode, um den Widerstand in kausal unterschiedliche Anteile zu zerlegen und ähnlichkeitsgetreu zu extrapolieren. Wichtige Beiträge dazu lieferten aber:

• Marc Beaufoy, der in London von 1796-1798 mehr als 1600 systematische Versuche in einem Hafenbecken vor allem an ebenen Platten (»plank tests«) und an einfachen Schiffsformen mit der fallenden Gewichtsmethode durchführte, oft auch tiefgetaucht, um den Reibungswiderstand dieser Objekte ohne Welleneinfluss festzustellen. Er wies entgegen damals noch vorherrschenden Vorurteilen nach, dass die Reibung oft einen wesentlichen Anteil des gesamten Widerstands darstellen konnte. Seine Ergebnisse, die leider erst spät vollständig veröffentlicht wurden (M. Beaufoy: »Nautical and Hydraulic Experiments«, hg. von Henry Beaufoy, London, 1834. Taschenbuch-Nachdruck, rarebooksclub.com, 2012.), hielten nachträglicher Prüfung durchaus Stand. Auch der Anteil des Hinterschiffs am Widerstand wurde als bedeutsam rehabilitiert.

• In Frankreich publizierten um 1850 Joseph Bertrand (1822–1900) und Ferdinand Reech (1825–1884, (F. Reech: »Cours de Mécanique«, Sektion V, S. 265-275, Paris, 1852.)) Notizen zur Ähnlichkeitsmechanik im Falle ge­forderter Ähnlichkeit der Schwerkräfte

in geometrisch und dynamisch ähnlichen Systemen. Reech wies auch auf die Ähnlichkeit von Wellenerscheinungen an Schiffen hin und forderte ein Schwerkraft-Modellgesetz, nach welchem Modellversuche bei »korrespondierender Geschwindigkeit« durchzuführen waren, um diesen Einfluss skalieren zu können. Für diesen Fall gab er ein Schwerkraft-Ähnlichkeitsgesetz an. Er befasste sich nicht näher mit anderen Widerstands­anteilen und führte, soweit bekannt, keine Extrapolationen durch.

• John Scott Russell (1808-1892), ein schottischer Ingenieur und Wissenschaftler, experimentierte früh mit Kanalbooten für die Passagier-Dampfschifffahrt zwischen Glasgow und Edinburgh. Er stieß dabei auf den Kanal- und Flachwasser­widerstandseffekt, den er mildern bzw. vermeiden konnte, indem er im überkritischen Bereich fuhr. Er erkannte die Bedeutung der Wellenenergieverluste für den Schiffswiderstand und entwickelte daraufhin seine »waveline theory«, die nach qualitativen Argumenten zu einer konkaven Vorschiffsform führte, die er dann aber auch für Schiffe auf tiefem Wasser propagierte (J. S. Russell: »The Waveline Principle of Ship Construction», Teil I und II, Trans. INA, Bd. I, 1860, S. 184–211, Teil III, Trans. INA, Bd. II, 1861,

S. 230–245.). Er führte dann für Projekte zahllose Modellversuche aus, es gelang ihm dennoch nicht, mit seiner Aufteilung in Widerstandsanteile eine praktikable Extrapolation auf die Großaus­führung zustande zu bringen. Daher gab Russell frustriert auf und erklärte die Ex­trapolation von Modellversuchen für nicht durchführbar. Er sprach sich stattdessen nur noch für Großversuche aus. Dessen ungeachtet gelang ihm offenbar, als später von 1854 bis 1859 auf seiner Werft in Milwall an der Themse der Segeldampfer »Great Eastern« von I. K. Brunel gebaut wurde, eine recht günstige Formgebung, ohne dass er sich dabei seiner »waveline theory« bediente.

• Eine hilfreiche, sachdienliche Rolle spielte in den Kontroversen um das Widerstandsproblem auch der Glasgower Physiker und Ingenieur William Rankine (1820–1872). Zum einen entwickelte er zur Bestimmung von Druckverteilungen und Stromlinienbildern an ebenen und achsensymmetrischen Körpern in paralleler Anströmung eine Singularitätenmethode, vor allem mit Quellen und Senken, die den Zeitgenossen anschau­liche Erklärungen für den Zusammenhang zwischen Form und Strömungsfeld lieferte. Rankine erkannte zum anderen die gewissermaßen gleichrangige Bedeutung von Zähigkeits- und Wellenwiderstand, aber auch das Phänomen der Ablösung und Wirbelbildung am Hinterschiff, und inspirierte damit wahrscheinlich Froude zu dessen Widerstandsaufteilung (W. J. M. Rankine: »On the Computation of the Probable Engine Power and Speed of Proposed Ships«, Trans. INA, Bd. 5, S. 316–333, 1864.).

4. William Froude

Aus Dartington, Devon, stammend, studierte William Froude (1810–1879) in den Jahren 1829 bis 1832 Mathematik in Oxford. Danach arbeitete er als Bauingenieur am Bau von Brücken und Eisenbahnen. Von 1837 bis 1846 wirkte er an Bauprojekten von Brunel für Eisenbahnen, Brücken und Schiffe mit, anschließend auch freiberuflich als Berater. Für Brunels »Great Eastern« untersuchte er z. B. das Rollschwingungsverhalten, die Reibung beim Querstapellauf, die Sogziffer und die Propellercharakteristik.

Durch diese Arbeiten und seine Vorträge erwarb Froude sich einen guten Ruf in der Fachwelt und wurde in der Zeit von 1864 bis 1870 von der British Association for the Advancement of Science für mehrere maritime Fachausschüsse als Experte herange­zogen. Dort arbeitete er mit Russell und Rankine zusammen und lernte auch die Ergebnisse von Reech zur »korrrespondierenden Geschwindigkeit« bei Schwerkraftähnlichkeit kennen. Reech wird in einem Ausschussbericht von 1870 zitiert, den Froude mitunterzeichnet hat, obwohl er den Namen Reech später nie erwähnte (T. Wright: »Ship Hydrodynamics 1710–1880«, Diss., unveröffentl., Dept. of Transport, Science Museum, South Kensington, London, und Dept. of the History of Science and Technology, The Univ. of Manchester, Institute of Science and Technology, Manchester, 1983.). Froude zog 1867 auf sein Grundstück Chelston Cross bei Torquay, Devon. Von dort aus führte er weitere Vorversuche durch, teils im kleinen Schlepptank mit fallenden Gewichten, teils im River Dart. Dazu gehören Geosim-Versuche mit Modellen von 3, 6 und 12 Fuß Länge mit zwei Schiffsformen, die er Raven und Swan nannte. Damit wollte er seine Extrapolationsmethode prüfen, die nun schon auf der Hypothese beruhte, dass der Reibungswiderstand und der Restwiderstand (d.h. Wellenwiderstand und Wirbelwiderstand ähnlich Rankine) näherungsweise trennbar und damit getrennt skalierbar sind. Die Modelle der beiden Formen wurden von einer Dampfbarkasse querab an langen Kragarmen gleichzeitig und damit bei gleicher Geschwindigkeit geschleppt.

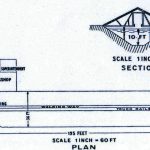
Die Ergebnisse ermutigten Froude, 1868 bei der Royal Navy einen Antrag auf Finanzierung für den Bau und Betrieb einer überdachten Modellversuchsrinne auf seinem Gelände bei Chelston Cross zu stellen. Der Antrag wurde 1870 (gegen die Opposition von Russell) mit einem Zuschuss von 2000 £ genehmigt und der Bau der Einrichtung 1871 nach 18 Monaten Bauzeit fertiggestellt. Froude konstruierte – und meist auch baute – seine Messapparaturen überwiegend selbst.

Der Tank von L x B x T = 85 x 11 x 3 m Abmessungen (Abb. 5) hatte einen Schleppwagen auf Schienen (Abb. 6), der von einer stationären Dampfmaschine über Seilzug angetrieben wurde. Die Messsysteme auf dem Schleppwagen ohne Besatzung dienten der automatischen Aufzeichnung von Daten der geschleppten Modelle in Widerstands-, Propulsions- und Freifahrtversuchen (Abb. 7). Der Wagen erreichte Geschwindigkeiten bis zu 5 m/s. Die Versuche mit geführten Modellen am Schleppwagen im überdachten Gebäude erwiesen sich als genauer und störungsfreier als zuvor im Freien mit fallenden Gewichten.

Außer der Begründung der ersten modernen Schiffsversuchsanstalt mit einem Schleppwagen auf Schienen und allen erforderlichen Messsystemen für den Widerstand und Antrieb von Modellen verdanken wir William Froude die wesentlichen Grundlagen der Ähnlichkeitsmechanik für die Extrapolation von Modellversuchsergebnissen. Die Froudesche Methode beruht auf der Hypothese, dass die Anteile des Widerstands, die auf Reibungskräfte und Schwerkräfte zurückgehen, näherungsweise physikalisch trennbar und damit nach unterschiedlichen Ähnlichkeitsgesetzen getrennt skalierbar sind (»Froudesche Hypothese«):

• Die Anteile des Gesamtwiderstands Rt waren nach Froude näherungsweise zwei unabhängige Terme, der Reibungswiderstand Rf und der Restwiderstand Rr, welcher den Wellenwiderstand Rw und den Wirbelwiderstand Rwi umfasste, d. h.

Rt = Rf + Rr =

= Rf + Rw + Rwi .

Dabei skalierte Froude nur den Term Rr nach dem Ähnlich­keitsgesetz (»law of comparison«) bei korrespondierender Geschwindigkeit.

• Der eigentlich neue, glanzvolle Beitrag von Froude war die »Froudesche Hypothese«, d. h. die Annahme, dass näherungsweise die Anteile Rf und Rr physikalisch trennbar sind, sodass man sie getrennt bestimmen und skalieren kann. Das führt, anders als bei früheren Widerstandstheorien, zu einem zweigliedrigen Ansatz, worin jeder Term nur von einem der Ähnlichkeitsparameter für Schwerkraft bzw. Zähigkeit beherrscht wird. Diese pragmatische Näherung unter Vernachlässigung von Wechselwirkungen ermöglichte damals wie heute den technischen Erfolg von Extrapolationsverfahren.

Dabei wird nach Froude der Restwiderstandsanteil nach dem Ähnlichkeitsgesetz (»law of similitude«) für Schwerkräfte bei korrespondierender Geschwindigkeit (bei gleicher Froude-Zahl in heutiger Terminologie) extrapoliert. Der Reibungswiderstand wird für Modell und Großausführung von Froude nach empirischen Verfahren ermittelt und getrennt skaliert.

Damit ist an die Stelle der eingliedrigen Widerstandsgesetze von Huygens, Newton und anderer ein zweigliedriger Ansatz für den Widerstand getreten, um die beiden Hauptursachen des Widerstands zu unterscheiden und jeden Anteil nach seinen eigenen Ähnlichkeitsgesetzen zu behandeln. Dieser Ansatz bleibt eine näherungsweise Hypothese und ist seitdem in vielfacher Hinsicht verfeinert und weiterentwickelt worden. Die Froudeschen Koeffizienten für den Reibungswiderstand sind überholt. Aber im Grundsatz hat sich die Froudesche Extrapolationsmethodik bewährt und bildet bis heute eine wertvolle Grundlage für das Schiffsmodell­versuchswesen.

William Froude verstarb schon 1878 nach nur acht Jahren wissenschaftlicher Arbeit mit immenser Produktivität an seiner Versuchsanstalt. Einen guten Überblick über Froudes Werk gibt der Gedächtnisband der Institution of Naval Architects (INA) mit seinen gesammelten Publikationen (A. D. Duckworth (Hg.): »The Papers of William Froude, 1810-1879«, INA, London, 1955.).

Das moderne Schiffsmodellversuchswesen hatte mit William Froude begonnen. Nach seinem Tod entstanden schon bis 1914 weltweit in vielen führenden Schiffbauländern 16 weitere Versuchsanstalten gleichen Typs, die meist relativ eng Froudes Einrichtungen nachahmten und seiner Methodik zur internationalen Durchsetzung verhalfen (s. (H. Nowacki: »Zur Vorgeschichte des Schiffbauversuchswesens«, Beitrag zum Sprechtag des FA Geschichte des Schiffbaus der STG, Bremerhaven, November 2013. Abgedruckt im STG-Jahrbuch 2013.)). Die deutsche Wissenschaft ist hierbei mit sechs Anstalten zahlreich vertreten.

5. Zusammenfassung

Archimedes legte in »On Floating Bodies« mit seinem Auftriebsprinzip und mit dem Hebelarmkonzept der Stabilität den Grund für die hydrostatische Bewertung der Schiffssicherheit, auch bis hin zu heute aktuellen Schadensszenarien.

William Froude überwand das Patt in der Extrapolationsfrage des Modellversuchswesens durch Einführung zweier, kausal getrennter Terme in der Widerstandsaufteilung, die nach unterschiedlichen Ähnlichkeitsgesetzen zu skalieren sind. Er schaffte auch apparativ den Anfang für ein modernes Modellversuchswesen.

Aus heutiger Sicht sucht man im Schiffsentwurf, aufbauend auf diesen Grundlagen, eine ganzheitliche Sicht auf die Anforderungen an die Wirtschaftlichkeit und Sicherheit von Schiffen. In der modernen Methodik des Risk-Based Ship Design (A. D. Papanikolaou (Hg.): »Risk-Based Ship Design. Methods, Tools and Applications«, Springer Publ., Berlin / Heidelberg, ISBN 978-3-540-89041-6, 2009.) führt man im Sinne probabilistischer Kriterien und ökonomischer Bewertung aller potenziellen Schadensereignisse an Mensch, Schiff mit Ladung und maritimer Umwelt die Einzelrisiken aller relevanten Risiko­szenarien in ein aggregiertes, ökonomisch bewertetes Gesamtrisiko zusammen. Dieser Wert wird verglichen mit dem akzeptierbaren Risiko, entweder nach dem Wert bei heutigen regelkonformen Schiffen oder nach neuen Grenzwerten, die bei der IMO noch in der Diskussion sind (s. (P. C. Sames: »Introduction to Risk-Based Approaches in the Maritime Industry«, Kap. 1, in: [23].)). Dann sucht man günstige Lösungen für eine Gesamtperspektive von Wirtschaftlichkeit und Sicherheit.Auch bei solchen anspruchsvollen modernen Entwurfsaufgaben spielen die wissenschaftlichen Grundlagen, die von Archimedes bis zu William Froude geschaffen wurden, noch immer eine wesent­liche Rolle.

Autor: Prof. Dr.-Ing. Dr. h.c. Horst Nowacki

Technische Universität Berlin, horst.nowacki@tu-berlin.de

Horst Nowacki