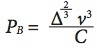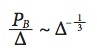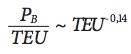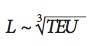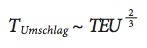Der Fluch der „Economies of Scale“

Hinter dem atemberaubenden Wachstum bei den Containerschiffsgrößen steht die Nutzbarmachung der Economies-of-Scale (EoS). Ulrich Malchow beschreibt in einer Fortsetzung seiner Analyse aus HANSA 07/2014, wie Linien die Folgen ihres Orderverhaltens zunehmend selbst zu spüren bekommen und hinterfragt den EoS-Effekt als Triebfeder für die gewaltigen Bestellungen der jüngsten Vergangenheit
Die Entwicklung bereitet nicht nur Häfen und Terminals zunehmend Probleme. Vor einem Jahr wurde bereits ausgeführt, dass der den Containerlinien[ds_preview] zugutekommende EoS-Effekt durch die mit wachsender Schiffsgröße überproportional wachsenden Infra- und Suprastrukturkosten mehr als kompensiert wird. So räumen selbst die CEOs großer Containerlinien mittlerweile im kleinen Kreis ein, dass das Größenwachstum der Schiffe zumindest volkswirtschaftlich längst keinen Sinn mehr macht. Allerdings kann sich keine Linie erlauben, sich dem Diktat der niedrigsten Slotkosten zu entziehen und aus der Spirale auszubrechen. Selbst der taiwanesische Carrier Evergreen, der sich jahrelang standhaft dem Größenwachstum widersetzt hat, ist eingeknickt und hat im Zuge seines Beitrittes zur CKYHE-Allianz elf 20.500-TEU-Schiffe bestellt.

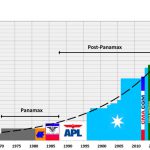
Die Abb. 1 gibt die bisherige Entwicklung der maximalen Schiffsgrößen in der Containerschifffahrt wieder. Es ist offensichtlich, dass Branchenprimus Maersk ab Mitte der 1990er Jahre der wesentliche Treiber dieser Entwicklung ist. Mit Ausnahme der USL-Jumbos in den frühen 80er Jahren, die für einen Round-the-World-Dienst gebaut worden waren, und den von HDW/Bremer Vulkan in den späten 80er Jahren für APL gelieferten ersten Post-Panamax-Schiffen zum Einsatz auf dem Pazifik, sind seit 40 Jahren alle Rekordschiffe für das Fahrtgebiet Europa-Fernost gebaut worden.

Das bisherige Größenwachstum der Containerschiffe folgt (zufällig?) mit hoher Regression (R2 = 0,945) einer Exponentialfunktion, die bekanntlich keinen Maximalwert hat! Demnach würden wir 2020 die ersten 23.000-TEU-Schiffe sehen; die 30.000-TEU-Marke wäre vermutlich ab 2025 in Sicht. Diese Größe verlangt nach aktueller Einschätzung einen Tiefgang von ca. 20m und dürfte aufgrund der Tiefe der Malakka-Straße, die auf der Europa-Fernost-Route stets zu passieren ist, als das praktisches Maximum der Größenentwicklung angesehen werden (Malaccamax). Schiffe für mehr als 21.150TEU sind bereits bestellt (OOCL) und es stellt sich die Frage, wie weit die Entwicklung tatsächlich noch auf dem Weg bis 30.000TEU voranschreitet.

Wirkung des EoS-Effektes

Der EoS-Effekt bewirkt, dass im Wesentlichen drei entscheidende spezifische Kostengrößen mit zunehmender Schiffsgröße sinken:

Investition pro TEU

Antriebsleistung pro TEU

Betriebskosten pro TEU (i.W. Personalkosten)

Investition pro TEU

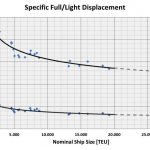
Schiffbau ist von seiner Natur letztlich »schwimmender Stahlbau«. Dies gilt umso mehr, je größer die Schiffe sind, da der Kostenanteil des Engineerings und der Ausrüstung mit wachsender Schiffsgröße abnimmt. Entsprechend lässt sich die verbaute Tonne Stahl als entscheidender Kostenparameter heranziehen (anstelle des von Marktgegebenheiten und Verhandlungsergebnissen geprägten Schiffspreises). Diesen Wert zu ermitteln, ist jedoch kein leichtes Unterfangen, da die reine Stahlmasse zumeist das Geheimnis der Designer und Werften bleibt. Hilfsweise kann jedoch die gesamte Leerschiffsmasse herangezogen werden, die sich im Wesentlichen aus der Stahlmasse und der Masse der Antriebsanlage zusammensetzt. Da alle Containerschiffe einer Größenklasse ein vergleichbares Geschwindigkeitsniveau aufweisen und damit ähnliche Antriebsleistungen erfordern, die stets durch denselben Typ Hauptmotor (Zweitakt-Langsamläufer) bereitgestellt wird, kann näherungsweise die gesamte Leerschiffsmasse als Parameter für den schiffbaulichen Aufwand in Form von verbautem Material herangezogen werden. Dank Archimedes entspricht die Leerschiffsmasse plus der stets bekannten maximalen Tragfähigkeit des Schiffes dem Deplacement auf maximalem Tiefgang, das zwar auch nicht generell publiziert ist, aber auf allen Capacity-Plänen und Pilot Cards eines Schiffes ausgewiesen ist.

Abb. 2 gibt für eine Auswahl aktueller Containerschiffe die spezifische Leerschiffsmasse und das spezifische Deplacement (auf max. Tiefgang) pro TEU inklusive einer Fortschreibung der Regressionskurven bis 30.000TEU wieder. Die Kurven haben (naturgemäß) einen asymptotischen Verlauf. Die Distanz zwischen beiden Kurven entspricht der Tragfähigkeit pro TEU. Es zeigt sich, dass die Leerschiffsmasse pro TEU und damit der bauliche Aufwand pro TEU mit der Schiffsgröße geringer wird aber in der Region > 20.000TEU praktisch nicht mehr sinkt und wohl nicht deutlich unter 3t/TEU kommt. Interessant ist, dass das Deplacement (auf max. Tiefgang) pro TEU mit der Schiffsgröße stärker sinkt, so dass auch die spezifische Tragfähigkeit (pro TEU) mit zunehmender Schiffsgröße geringer wird und bei 30.000TEU weniger als 10t/TEU betragen dürfte. Das heißt, die zusätzlichen Stellplätze, deren Herstellung praktisch nicht mehr günstiger wird, sind auch noch weniger »wertvoll«.

Antriebsleistung pro TEU

Die installierte Antriebsleistung ist in zweifacher Hinsicht ein wichtiger Parameter: Einerseits kann mit der ausnahmslos zur Anwendung kommenden Langsamläufer-Zweitakt-Technologie der tägliche Brennstoffverbrauch und damit der entscheidende Bunkerverbrauch als proportional zur Antriebsleistung angesetzt werden. Andererseits ist auch die Masse der Antriebsanlage, die ein Bestandteil der Leerschiffsmasse ist, eine Funktion ihrer Leistung.

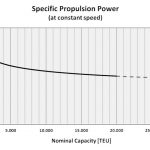
Nach der klassischen Admiralitätsformel wächst die Antriebsleistung PB bei konstanter Geschwindigkeit v nur unterproportional zur Schiffsgröße (genauer: Deplacement ), was bereits einen Großteil des EoS-Effektes ausmacht (C ist die sogenannte »Admiralitätskonstante«):

Bildet man hieraus die auf die Schiffsgröße (Deplacement) bezogene spezifische Antriebsleistung PB/ , ergibt sich auch hier eine asymptotische Proportionalität:

Da die Regressionsfunktion für das Deplacement aus der (nominellen) TEU-Kapazität (Abb. 2) schon einen unterproportionalen Charakter hatte, wächst die Antriebsleistung nur noch quasi »doppelt unterproportional« mit der TEU-Kapazität, was die Kurve der spezifischen Antriebsleistung pro (nominellem) TEU mit wachsender TEU-Kapazität noch flacher werden lässt. Abb. 3 zeigt den qualitativen Verlauf für eine beliebige Geschwindigkeit.

Betriebskosten pro TEU

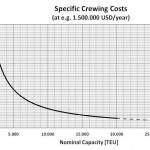
Größter Bestandteil der Betriebskosten sind die Kosten für die Besatzung, die im betrachteten Größenspektrum als grundsätzlich schiffsgrößenunabhängig anzusehen sind. Dass die Kosten eines 2.000-TEU-Schiffes in der Praxis dennoch geringer sind als die eines 14.000-TEU-Schiffes – wie aus der »HANSA Schiffsbetriebskostenstudie 2014« hervorgeht – mag darin begründet sein, dass die großen Schiffe sich eine teure Flagge mit entsprechender Besatzungsstruktur eher »leisten« können und/oder mit einem aufwendigeren Maintenance-Konzept betrieben werden. Bei fixen jährlichen Besatzungskosten von z. B. 1,5Mio. $ ergibt sich naturgemäß erneut ein asymptotischer Verlauf der jährlichen spezifischen Kosten pro TEU, wie Abb. 4 zeigt.

Resümee Aufwandsgrößen

Es lässt sich konstatieren, dass alle wesentlichen spezifischen Aufwandsgrößen (Leerschiffsmasse pro TEU, Antriebsleistung pro TEU, Besatzungskosten pro TEU) einen stark asymptotischen Verlauf aufweisen, der bei weiterem Größenwachstum nur noch marginale spezifische Kostenvorteile verspricht.

Gleichzeitig bereiten die wachsenden Schiffsgrößen den Häfen und Terminals (und selbst den Kunden der Linien) zum Teil erhebliche Probleme, indem sie dort erhebliche Mehrkosten verursachen (ohne deswegen insgesamt mehr Container umzuschlagen), die gar überproportional zur Schiffsgröße wachsen. Dieser Umstand ist mittlerweile erkannt und sogar von der OECD in einer Studie beleuchtet worden.

Neben nur noch marginalen Einsparungen erwachsen den Linien selbst aber auch zusätzliche Kosten aus dem Größenwachstum der Schiffe. Dazu zählen Frachtratenverfall, Kosten der Unterauslastung, Wertverlust der Bestandsflotte, operationelle Kosten, Liegezeit und Versicherungsprämien durch Klumpenrisiko.

Frachtratenverfall

Das »all-time low« der Containerfrachtraten ist zwar keine direkte Folge der generellen Schiffsgrößenentwicklung, wohl aber ihrer Geschwindigkeit und des verbundenen Neubauvolumens, das zu einem extremen Überangebot an Slotkapazität geführt hat – mit entsprechenden Konsequenzen für die Raten.

Unterauslastung

Bei einem Sprung von z.B. 14.000 auf 18.000TEU sollen sich die Slotkosten gemäß Berechnungen der Klassifikationsgesellschaft DNV GL um 9% reduzieren. Dieser EoS-Effekt kommt aber nur zum Tragen, wenn die Schiffsauslastung konstant bleibt. Kommen weiterhin nur 14.000TEU zur Verladung (Auslastung: 78%), liegen die Kosten pro TEU gar 15% höher als beim kleineren Schiff! Die »Downside« ist grundsätzlich größer als die »Upside«. Angesichts der vorherrschenden und noch viele Jahre anhaltenden Überkapazitäten ist das Risiko, unter der »Downside« zu leiden größer als die Chance von der »Upside« zu profitieren.

Bestandsflotte

Der Kaskadeneffekt führt dazu, dass nach der Infahrtsetzung immer größerer Schiffe im Europa-Fernost-Verkehr die dort vorhandenen Schiffe in andere Fahrtgebiete verlegt werden, wo weitere Verdrängungseffekte einsetzen. Diese Verlegungen sind alles andere als nachfragegetrieben. Entsprechend sind die Frachtraten überall unter Druck. Damit einher geht ein dramatischer Wertverlust bei der gesamten Bestandsflotte. Diese Verluste, obwohl einzelnen Marktteilnehmern kaum zuzuordnen, müssen in ihrer Gesamtheit eigentlich den Neubaupreisen zugeschlagen werden.

Operationelle Kosten

Mit der wachsenden Schiffsgröße wachsen auch die operationellen Schwierigkeiten, die auch Kosten auf Seite der Linien verursachen. In Tidehäfen wird durch kleinste Verzögerungen oft eine ganze Tide verloren, da die einzuhaltenden Zeitfenster immer kleiner werden. 50% der Tageskosten des Schiffes fallen dann konsequenterweise als Verzögerungskosten an (zuzüglich der Kosten für damit meistens einhergehende Verholmanöver).

Liegezeit

Es ist trivial, aber große Schiffe liegen grundsätzlich länger im Hafen. Da nach dem kubischen Gesetz die Länge des Schiffes grundsätzlich nur unterproportional zur Schiffsgröße wächst, kann auch die Anzahl der einsetzbaren Containerbrücken nicht proportional zur TEU-Kapazität gesteigert werden:

Bei konstanter Umschlagrate pro Brücke steigt somit grundsätzlich die Umschlagzeit eines Containerschiffes mit seiner Größe (wenngleich unterproportional):

Es kommt jedoch hinzu, dass der einzelne Umschlagvorgang bei einem großen Schiff deutlich mehr Zeit in Anspruch nimmt, da der durchschnittliche Weg jedes Containers deutlich länger ist (+ ca. 40% bei einem 19.000-TEU-Schiff gegenüber einem Panamax-Schiff von 4.800TEU). Entsprechend geringer würde die Umschlagrate bei unveränderter Hub- und Katzgeschwindigkeit der Brücke ausfallen. Daher würde die Gesamtumschlagzeit mindestens linear mit der Schiffsgröße ansteigen.

Es ist daher kein Wunder, dass die Linien ihre Terminals drängen, durch Anwendung von diverser »Umschlagakrobatik« (z.B. schnelle Hub- und Katzfahrwerke, Zwei- oder gar Drei-Katz-Brücken, Vier-TEU-Spreader, Dual-Cycle-Verfahren) die Umschlagrate pro Brücke zu erhöhen, damit sich der Anstieg der Gesamtumschlagzeit bei den Mega-Schiffen in Grenzen hält.

Bei unveränderter Rundreisedauer und Hafenfolge verursacht die zusätzliche Hafenzeit durch Upspeeding einen erheblichen Anstieg der Bunkerkosten pro Rundreise. Wenn dies aufgrund nicht mehr vorhandener Geschwindigkeitsreserve nicht möglich sein sollte, muss sogar die Schiffsanzahl erhöht werden. Erhöht sich z.B. auf einer ursprünglich elfwöchigen Fernost-Rundreise die kumulierte Hafenzeit um eine Woche, müßte bei wöchentlichen Abfahrten ein zusätzliches zwölftes Schiff eingesetzt werden!

Klumpenrisiko

Auch Versicherer sehen die Schiffsgrößenentwicklung zunehmend kritisch, da sich das »Klumpenrisiko« drastisch erhöht, mit entsprechenden Auswirkungen auf die Versicherungsprämie. Immerhin würde der Totalverlust eines beladenen Mega-Carriers mit einer bis 1,5 Mrd. $ zu Buche schlagen.

Fazit

Wenn die genannten Kostenpositionen der Carrier objektiv bei zudem realen Auslastungen und nur noch marginalen Kostenvorteilen des Größenwachstums saldiert würden, käme wahrscheinlich heraus, dass selbst die bereits in Fahrt befindlichen Mega-Schiffe schon längst keinen größenbedingten Vorteil mehr aufweisen. Die zusätzlich von anderer Seite (Terminals, Häfen, Kunden) zu tragenden erheblichen Kosten des Größenwachstums machen es aus gesamtwirtschaftlicher Sicht schon längst sinnlos.

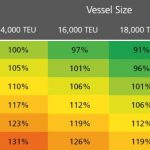
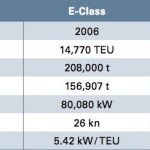
In einer Replik zum jüngst veröffentlichten Bericht der OECD »The Impact of Mega-Ships« widerspricht Maersk allerdings, indem angeführt wird, dass die Slotkosten seiner Triple-E-Schiffe (18.270TEU) bis zu 500$ unter denen eines 14.000-TEU-Schiffes liegen (womit wohl die eigene E-Class gemeint sein dürfte). Tatsächlich ist allein bei der spezifischen Antriebsleistung, als eine der wesentlichen Aufwandsgrößen (der Bunker­verbrauch ist hierzu proportional), eine beachtliche Einsparung von 40% zu verzeichnen (Tab. 1). Berechnungen des Autors ergeben jedoch, dass hiervon nur ca. 7% dem EoS-Effekt zugerechnet werden können. 33% beruhen demnach auf der reduzierten Geschwindigkeit (und auch dem verbesserten Maschinenwirkungsgrad) und sind daher alles andere als größenbedingt!

Es ist ein bemerkenswertes Phänomen, dass eine ganze Branche die Bedrohung ihres Handelns (auch für die eigene Existenz) zwar erkennt, aber nicht in der Lage ist, selbst gegenzusteuern, sondern in einer selbstmörderischen Spirale gefangen ist. Insofern steht zu vermuten, dass die Containerlinien sogar erleichtert wären, wenn sie durch Einführung eines von außen gesetzten Größenlimits von dem Investitionszwang in immer größere Schiffe befreit würden und nicht erst bei 30.000TEU (Malaccamax) Schluss ist. Hierzu wäre allerdings vorzugsweise die konzertierte Aktion einiger Häfen gefragt, denen das Größenwachstum die größten Probleme bereitet. Ein diesbezüglicher »Notanker« ist der Suez-Kanal. Für dieses von allen Europa-Fernost-Schiffen zu passierende Nadelöhr besteht kein explizites Tiefgangslimit, sondern es ist ein maximaler Unterwasserquerschnitt festgelegt, der erst 2010 auf den aktuellen Wert erhöht worden ist. Dieser besagt, dass zum Beispiel »MSC Oscar«, als das derzeit größte Containerschiff der Welt (19.224TEU) mit einer Breite von 59m (23 Containerreihen quer) einen Tiefgang von maximal 17,04m aufweisen darf.

Bei ihrem tatsächlichen Festigkeitstiefgang von 16,0m ist also noch Luft. Bei unveränderter Breite und Hinzufügen einer 40-ft-Bay könnten sogar rund 22.000TEU dargestellt werden. Bei einer Verbreiterung um eine Containerreihe auf 61,5m darf der Tiefgang laut Suez-Vorschriften jedoch nur noch 16,3m betragen, was nicht mehr ganz ausreichen dürfte. Insofern wäre sehr zu hoffen, dass der Kanal trotz seines gegenwärtigen Ausbaues sein Querschnittslimit beibehält und sich somit ein Größenlimit von zumindest circa 22.000TEU einstellt.

Prof. Dr.-Ing. Ulrich Malchow